আশ্চর্য টালির আখ্যান

পুজোর আগে জোর কদমে বর্ধমানের শ্যামলালে আমার বাড়ির সামনের রাস্তায় টালি পাতার কাজ শুরু হয়েছিল। অর্ধেকের‌ও কম রাস্তায় টালি পেতেছে কি পাতে নি, ঝমঝমিয়ে এমন বৃষ্টি শুরু হল যে আর বলার নয়। টালি দিয়ে ছাইবার আগেই জল দিয়ে এমন ছেয়ে দিল রাস্তাটা যে তাকিয়ে দেখলে যে কেউ বলবে এটাই সুয়েজ খাল। আর আমি হয়ে গেলাম পাক্কা দুইদিন ঘরবন্দী। কী আর করি, সারাদিন তাই টালি দিয়ে ছাইবার ছাঁইপাশ ফন্দী ভাবতে ভাবতে গুগল জ্যাঠার ঘরে উঁকি মারলাম।

ও বাবা, দেখি টালি নিয়ে এবং ছাইবার ধরনধারন নিয়ে বিস্তর গবেষণা হয়েছে এবং হয়েও চলেছে! টালি, অর্থাৎ ইংরেজরা যাকে "Tiles" লেখে, তা দিয়ে কোনো তলকে (surface) ছাইবার, মানে ভদ্রভাষায় আচ্ছাদন করার যে প্রক্রিয়া, তার নাম হচ্ছে "টাইলিং" (tiling)। এখানে 'তল' মানে দ্বিমাত্রিক (2D) তলের কথাই ধরা হল, তা সে সমতল (plane) হোক কি বক্রতল (curved surface)। কিন্তু এ তো গেল টালির মিস্ত্রীর কথা। মজা লাগল এইটা জেনে যে এরকম একটা তলকে কতরকমভাবে এবং কতটা দক্ষতার সঙ্গে নির্দিষ্ট জ্যামিতিক আকৃতির টালি দিয়ে আচ্ছাদিত করা যায়, তাই নিয়ে অঙ্কের লোকেরা "টাইলিং" নামের আস্ত একটা অধ্যায় খুলে ফেলেছে।

হাজার বছরের‌ও বেশি সময় ধরে আমরা দেখেছি যে ত্রিভুজ বা ষড়ভুজের মত আকারের টালি দিয়ে কোনো তলকে সাজালে সাজানোটা একেবারে নিখুঁত হয়। একটু ভেবে দেখলে বোঝা যাবে যে খুঁত বলতে আমরা আসলে বুঝি এবড়োখেবড়ো বা অসমান আকার আর এলোমেলো ফাঁকা জায়গাকে— ত্রিভুজ, চতুর্ভুজ বা ষড়ভুজ টালির ক্ষেত্রে যেগুলো একেবারেই থাকে না। আরো ভালোভাবে বললে, টালির সজ্জাটা পর্যায়ক্রমে পুনরাবৃত্ত হয়। উদাহরণস্বরূপ, একটা মৌচাকের ষড়ভুজাকৃতি গঠনের দিকে তাকিয়ে দেখলে বিষয়টা স্পষ্ট হবে। এখানে এক-একটা ষড়ভুজ প্রকোষ্ঠ (hexagonal cell) হচ্ছে এক-একটা টালি। প্রতিটা প্রকোষ্ঠের মধ্যে একটা করে ষড়ভুজাকার ফাঁক থাকলেও কোনো দুটো প্রকোষ্ঠের মাঝখানের জায়গায় কোনো ফাঁক নেই, একটা প্রকোষ্ঠ (পড়ুন, টালি) আরেকটা প্রকোষ্ঠের একেবারে গায়ে গায়ে লেগে আছে। টালিতে টালিতে ফাঁক নেই, সব দিকে কেমন একটা সমতা বিরাজ করছে।

পক্ষান্তরে, গত শতাব্দীর আশির দশকে কয়েকজন বিজ্ঞানীর গবেষণায় "পেনরোজ টাইলিং" নামে একরকম টাইলিং পদ্ধতি জানা যায়। এই পদ্ধতিতে টালিগুলোর সাজানোর মধ্যে আগের মত পর্যায়ক্রমিক সজ্জা অনুপস্থিত। এরকম টাইলিং যে প্রকৃতিও ব্যবহার করে থাকে, তা জানা যায় ১৯৮২ সালে যখন রসায়নবিদ ড্যান শেচম্যান (Dan Shechtman) অ্যালুমিনিয়াম আর ম্যাঙ্গানিজের উপরে গবেষণা করতে গিয়ে এমন অ-পর্যায়ক্রমিক "টালি-ছাওয়া" (tiling-এর পাতি বাংলা পরিভাষা, আর কি) পদ্ধতি লক্ষ্য করেন। বলা বাহুল্য, এক্ষেত্রে দ্বিমাত্রিক (2D) তলের বদলে আমাদের ত্রিমাত্রিক (3D) স্থান ভাবতে হবে, আর টালিগুলো‌ও অবশ্যই 3D হবে, কারণ এটা বাস্তব জগতের পদার্থ যার দৈর্ঘ্য, প্রস্থ এবং উচ্চতা তিনটে মাত্রাই আছে। নুন এবং আরো অনেক রকম কেলাসে আয়ন বা পরমাণুদের যেমন পর্যায়ক্রমিক সজ্জা দেখা যায়, শেচম্যানের গবেষণায় তার উল্টো ধরনের কেলাসের কথা জানা যায়। এটাও কেলাস, তবে পর্যায়ক্রমিক সজ্জা না থাকার জন্য এর নাম দেয়া হয় "কোয়াসি-ক্রিস্টাল" (Quasicrystal) বা ছদ্ম-কেলাস। প্রথমদিকে তাবড় তাবড় রসায়নবিদ মোটেও মানতে চান নি যে প্রকৃতিতে এরকম ছদ্ম-কেলাস থাকতে পারে। সে আরেক অসম লড়াইয়ের ইতিহাস। অবশেষে এই ২০১১ সালে শেচম্যান কোয়াসি-ক্রিস্টালে বিশদ গবেষণার স্বীকৃতি হিসাবে রসায়নে নোবেল পুরস্কার পেয়েছেন।

তাহলে এমনি কেলাস হোক কিংবা দ্বিমাত্রিক তল, আমাদের টালি-ছাওয়া পদ্ধতির মূলতঃ দুটো বৈশিষ্ট্য আছে:

১. পাশাপাশি টালিদের মধ্যে ফাঁক থাকছে না, টালিরা একে অপরের গায়ে লেগে 2D তল বা 3D শূন্যস্থান ভরাট করে তুলছে।

২. এইভাবে টালি সাজালে দুইরকম সজ্জা পাওয়া যাচ্ছে— পর্যায়ক্রমিক (periodical) এবং অ-পর্যায়ক্রমিক (non-periodical), এবং প্রকৃতিতে দুই ধরনের সজ্জাই দেখতে পাওয়া যায়। পর্যায়ক্রমিক সজ্জায় একরকম টালি হলেই চলছে। কিন্তু অ-পর্যায়ক্রমিক সজ্জায় বেশিরভাগ ক্ষেত্রে দরকার একের বেশি রকমের টালি।

এক রকমের টালি ব্যবহার করেও যে অ-পর্যায়ক্রমিক সজ্জা বানানো সম্ভব তার গাণিতিক ধারণা এই ২০২৪ সালেই দিয়েছেন নিউইয়র্কের গণিতজ্ঞ গুডম্যান-স্ট্রাস এবং অন্যান্যরা।

এইসব ভারি ভারি বিষয় জানার পরে গোল গোল ফর্সা ফর্সা সাদা ফুলকো লুচি আর গোলমরিচ-হিং দিয়ে সাদা আলুর তরকারি খাচ্ছি। আমার স্বরাষ্ট্রমন্ত্রী আমার পেটের কথা ভেবে প্রথমে চারটে লুচি দিয়েছিলেন। পরে তাঁর চোখ এড়িয়ে রান্নাঘরে আরো দুটো ফুলকো লুচি ম্যানেজ করতে যাই। গিয়ে দেখি একটা বড় ডেকচির মধ্যে গোটা কুড়ি ফর্সা গোলক ভাসছে। ভাসছে, কারণ লুচিগুলো ফুলকো, একটা আরেকটার একেবারে গায়ে গায়ে লেগে যায় নি তখন‌ও, সামান্য ছুঁয়ে আছে। উপর থেকে দেখে তাই মনে হচ্ছে উপরের লুচিগুলো নীচের লুচিগুলোর উপরে ভেসে রয়েছে! এইসব দেখে আমার মোটা মাথায় ফের একটা প্রশ্নের উদয় হল। আচ্ছা, কেউ কি কোনোদিন বৃত্ত (circle) দিয়ে 2D তল বা গোলক (sphere) দিয়ে 3D তল ভরাট করার কথা ভেবেছে! এক্ষেত্রে ফাঁক না থেকে যায় কি করে! যদিও এই ফাঁকে স্বরাষ্ট্রমন্ত্রী ডেকচিটা ঢাকা দিয়ে আর আমার নিত্য পৈটিক গোলযোগের কথা স্মরণ করিয়ে রান্নাঘর থেকে খেদিয়ে দিলেন, আমার মনে গোল গোল টালির ব্যাপারটা থেকে গেল। যথারীতি গুগলিয়ে দেখার চেষ্টা করলাম বিষয়টা।

ছোটোবেলায় জিগ-স ধাঁধা বা পাজ্ল (Jigsaw Puzzle, জিগ-স মানে একরকম করাত, কার্ডবোর্ডের উপর ছবি এঁকে সেই ছবিকে জিগ-স করাত দিয়ে ইচ্ছেমত সরলরেখা এবং বক্ররেখা বরাবর কেটে ফেলা হয়, তারপর অন্য কাউকে ডেকে সেই টুকরোগুলো ঠিকঠাক সাজিয়ে আগের ছবিতে ফিরিয়ে আনতে বলা হয়) আমরা অনেকেই সমাধান করেছি। কখনো পৃথিবীর ম্যাপ, কখনো আলিবাবা-চল্লিশ চোরের কাহিনী অনুসারে আঁকা ছবি সাজানো। এই ধাঁধার টুকরোগুলো সবসময় একেবারে আয়তাকার বা বর্গাকার হত না। একটা বর্গাকার বা আয়তাকার টুকরোর একদিকের বাহু থেকে টিউমারের মত একটা উত্তল গোলাকার গঠন বেরিয়ে থাকত। আবার এর সঙ্গে যে টুকরোটা আটকাবে তার একদিকের বাহুতে এমন একটা জায়গায় একটা অবতল গোলাকার খাদ থাকত। আগের টুকরোটার উত্তল গঠন পরের টুকরোটার অবতল গঠনে খাপে খাপ ঢুকে যেত আর টুকরোদুটো একটার সঙ্গে আরেকটা আটকে যেত। অর্থাৎ গোলাকার গঠন দিয়ে 2D তল ভরাট করতে হলে ফাঁকগুলোতে ঐরকম কোনো ব্যবস্থা রাখতে হবে। টালির আকার পুরোপুরি বৃত্ত হলেও চলবে না, আবার পুরোপুরি নিয়মিত আকার হলেও চলবে না।

এখানে জানিয়ে রাখা দরকার যে গণিতের ভাষায় ত্রিভুজ, চতুর্ভুজ, পঞ্চভুজ, ষড়ভুজ ইত্যাদি একসঙ্গে আদর করে 'বহুভুজ' (polygon, gon মানে বাহু, poly মানে একের বেশি) বলেই ডাকা হয়। সেই দিক দিয়ে দেখতে গেলে বহুভুজের বাহু ছয়, সাত,..., একশো, দুশো এরকম করে বাড়তে বাড়তে একেবারে অসীমের কাছাকাছি পৌঁছে গেলে ওটা আসলে একটা বৃত্তের মত‌ই মনে হবে। সুতরাং বৃত্ত ব্যাটাও আসলে একটা বহুভুজ, যার বাহু সংখ্যার কোনো লেখাজোকা নেই। এ তো গেল দ্বিমাত্রিক তলের কথা। ত্রিমাত্রিক স্থানে আমাদের যে 3D টালি দরকার, সেই টালিগুলোর ভুজ বা বাহু নিয়ে আমাদের মাথাব্যথা করার প্রয়োজন নেই। আমাদের বরং হিসাব রাখতে হবে 3D টালিগুলোর কয়টা তল আছে। যেমন ত্রিভুজ হচ্ছে 2D, এর 3D অনুরূপ পিরামিড কিংবা ত্রিকোণাকার প্রিজম। পিরামিডের চারটে ত্রিভুজাকৃতি তল আছে। ত্রিকোণাকার প্রিজমে দুটো ত্রিভুজাকার আর তিনটে আয়তাকার তল আছে। তলের গ্রীক নাম কিনা হেড্রা (hedra), আর তাই পিরামিডের নাম টেট্রাহেড্রন (tetrahedron, tetra মানে চার, four, 4)। একের বেশি হেড্রা আছে এমন 3D আকারকে তাই বলে পলিহেড্রন। এইভাবে হেড্রা বা তলের সংখ্যা বাড়তে বাড়তে একসময় অসীমের কাছাকাছি পৌঁছে গেলে পাওয়া যাবে 2D বৃত্তের 3D অনুরূপ— গোলক।

সাধারণ বুদ্ধি বলে, গোলক দিয়ে 3D স্থান যদি ফাঁক-বিহীনভাবে (gap less) ভরাট করতে হয়, তবে আমাদের গোলকটাকে নমনীয় জ্যামিতিক বস্তু হিসাবে কল্পনা করতে হবে। অর্থাৎ ফুলকো লুচির মত ভঙ্গুর গোলক নয়, ময়দার গুটির মত নমনীয় গোলক আমাদের দরকার, যাদের ঠাসলে তারা একটা আরেকটার গায়ে চেপ্টে তাদের মাঝের ফাঁকা জায়গাগুলো পর্যন্ত ভরাট করে ফেলতে পারবে। এইভাবেই তো ট্রে-র উপরে ময়দার গুটি সাজিয়ে বেকিং করলে গায়ে গা লাগানো একসারি গোলাকার বান রুটি পাওয়া যায়। এইখানে লক্ষ্য করলে দেখা যাবে আসলে বান রুটিগুলো সম্পূর্ণ গোলক নয়। রুটিগুলো যে জায়গায় একটার সঙ্গে আরেকটা জুড়ে রয়েছে সেই জায়গাটায়, মানে কিনারায় (corner), বৃত্তচাপ সোজা হতে হতে প্রায় সরলরেখায় পরিণত হয়েছে।

এখন এই রুটিগুলো যদি ত্রিমাত্রিক টালি হয়, তবে বোঝাই যাচ্ছে যে এক্ষেত্রে টালির প্রকৃতি একেবারে নমনীয়, যেমন ভাবে চাই তেমন ভাবে তাকে বেঁকিয়ে-বাঁকিয়ে আরেকটা টালির গায়ে বসিয়ে জায়গা ভরাট করে দেয়া যায়। গণিতজ্ঞেরা এইরকম নমনীয় টালির নাম দিয়েছেন সফ্ট সেল (soft cell), অর্থাৎ কিনা নমনীয় কোষ। সফ্ট সেল ব্যবহার করে টাইলিং পদ্ধতি, যাকে এককথায় বলে সফ্ট টাইলিং (soft tiling), সেই পদ্ধতিতে টালি সাজালে আমরা পাব পর্যায়ক্রমিক সজ্জা।

ব্যাপারটা আরেকটু খোলসা করে লেখা যাক। নিয়মিত জ্যামিতিক আকারের বস্তুদের আকৃতি দৃঢ় (rigid), যা চট করে পাল্টানো যায় না। "তাসের ঘর" নাটকের তাসগুলোর মত এরা নিয়মনীতি মেনে চলে। নমনীয় টালি অর্থাৎ সফ্ট সেলদের সেই নিয়মের বালাই নেই — ওরা "যেখানে যেমন সেখানে তেমন, যখন যেমন তখন তেমন" গোত্রের অন্তর্ভুক্ত।

হাঙ্গারির রাজধানী বুদাপেস্টের 'ইউনিভার্সিটি অফ টেকনোলজি অ্যান্ড ইকোনমিক্স'-এ গণিতবিদ গেবর ডোমোকোস এই ধরনের সফ্ট সেলের জ্যামিতি নিয়ে গবেষণা করছিলেন। এই বছর অর্থাৎ ২০২৪ সালে বিখ্যাত নেচার সাময়িকীতে ডোমোকোস এই সফ্ট সেল নিয়ে নতুন একরকম অঙ্ক কষে দেখিয়েছেন যে ঠিক কিভাবে নিয়মিত জ্যামিতিক গঠনের একটা টালি তার কিনারা (corner) পরিবর্তন করে করে একটা সফ্ট সেলে পরিণত হয়।

দ্বিমাত্রিক বা 2D তলে বৃত্তদের সফ্ট সেল হিসাবে ব্যবহার করলে দেখা যাবে একটা সেল আরেকটা সেলের সঙ্গে খাপে খাপ আটকাতে সেকেন্ড ব্র্যাকেটের মত একরকম খাঁজ বা চূড়া তৈরি করেছে— এই ধরনের কিনারার আকারকে ইংরেজিতে বলে কাস্প্ (cusp)। যে কোনো কাস্পের অন্তঃকোণ (internal angle) শূন্য, ঐ জায়গাটা ক্রমশঃ সরু ছুঁচালো হতে হতে পাশের সেলের একপাশে গিয়ে ঠেকেছে। গণিতবিদ ডোমোকোস দেখেছেন যে 2D তলে নমনীয় কোষ তৈরি করতে হলে টালিগুলোর কমপক্ষে দুটো এইরকম কাস্পের মত ছুঁচালো গঠন থাকা জরুরি। (দেখুন, চিত্র ১)

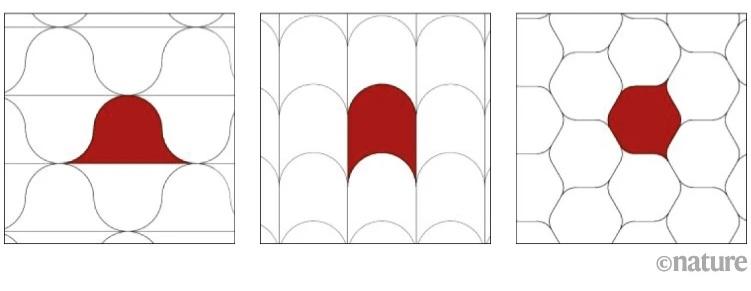
চিত্র ১: দ্বিমাত্রিক সফ্ট সেলের উদাহরণ

ডোমোকোসেরা গবেষণা করে দেখাচ্ছেন যে প্রকৃতিতে 2D তলের উপর এরকম নমনীয় টালির উদাহরণ অনেক রয়েছে। নদী যেখানে অনেক ধারায় প্রবাহিত হয়ে সাগরে মিশেছে, সেখানে নুড়িপাথর জমে জমে যে ব-দ্বীপ তৈরি হয়, তার বিশেষ 'ব'-আকারের পিছনে আসলে ঐ সফ্ট সেলের কাস্পের মত ছুঁচালো গঠন দায়ী। এখানে এক একটা দ্বীপ এক একটা সফ্ট সেলের মত আচরণ করছে। কখনো পেঁয়াজ আড়াআড়ি সরুভাবে কেটে চাকা চাকা বানিয়েছেন স্যালাডের জন্য? ডোমোকোসদের গবেষণা জানাচ্ছে, ভালো করে ঐ একটা চাকা পেঁয়াজের দিকে তাকালে ভিতরে আরো ছোটো ছোটো চাকা পেঁয়াজের টুকরো দেখা যাবে, যারা এক একটা সফ্ট সেল হিসাবে একটা আরেকটার গায়ে লাগিয়ে সাজানো আছে। আমাদের ঠোঁট, জিভ, বা ত্বকের বাইরের দিকে যে আবরণী কলা (Epithelial tissue) থাকে তার যদি একটা প্রস্থচ্ছেদ (cross-section) নেয়া যায় তবে তাতে এই কোষগুলোও 2D সফ্ট সেলের মত সাজানো থাকে। (দেখুন, চিত্র ২)

চিত্র ২: প্রাকৃতিক সফ্ট সেলের কিছু দৃষ্টান্ত

3D সফ্ট সেলের একটা উদাহরণ ইতোমধ্যে দেয়া হয়েছে গোল বানরুটির সারি দিয়ে। সেটা মানুষের তৈরি। এখানে কিন্তু কোনো কিনারাই ছুঁচালো নয়। এইটা একটা তফাৎ 2D সফ্ট সেলের সঙ্গে 3D সফ্ট সেলের। ত্রিমাত্রিক স্থানে প্রকৃতি কোনো খাঁজ রাখতে চায় না। কারণ ছুঁচালো অংশ রাখা মানেই গঠনটা দুর্বল এবং ভঙ্গুর হয়ে পড়বে। প্রকৃতির বানানো এমন 3D সফ্ট সেলের একটা উদাহরণ গেবর ডোমোকোস দিলেন সামুদ্রিক প্রাণী 'নটিলাস'-এর দেহের গঠন দেখাতে গিয়ে। নটিলাস আসলে শামুকের মত একরকম প্রাণী। তার খোলসের প্রস্থচ্ছেদের জ্যামিতি বিশ্লেষণ করতে গিয়ে প্রথমে মনে হয়েছিল, কোষগুলোর 2D সফ্ট সেলের মত ছুঁচালো কিনারা থাকতে পারে। পরে 3D আকার দেখে বোঝা গেল সেলগুলোর কোনো কিনারাই ছুঁচালো নয়। (দেখুন, চিত্র ৩)

চিত্র ৩: সামুদ্রিক প্রাণী নটিলাসের খোলসের প্রস্থচ্ছেদ

শুরু করেছিলাম পাড়ার রাস্তায় টালি পাতার কাজ দিয়ে। অর্থাৎ সিভিল এঞ্জিনিয়ারদের ব্যাপার-স্যাপার নিয়ে। লেখা শেষ করি তাঁদের‌ই নিয়ে। স্থাপত্য শিল্পে ত্রিমাত্রিক স্থানে সফ্ট টাইলিং-এর প্রয়োগ যদি দেখতে ইচ্ছে হয় তবে আমাদের যাওয়া উচিত আজারবাইজানের রাজধানী বাকু-তে। এখানে বিখ্যাত স্থপতি জাহা হাদিদের ডিজাইন করা হায়দার আলিয়েভ সেন্টার-এর বাড়িটার ছবি নীচে দেয়া হল। ডোমোকোসদের দাবী, সফ্ট টাইলিং-এর অঙ্ক না জেনেও হয়ত জাহা হাদিদ এই অদ্ভুত ছাদ-ওয়ালা বাড়িটা বানিয়েছেন। (দেখুন, চিত্র ৪)

চিত্র ৪: হায়দার আলিয়েভ সেন্টার, বাকু, আজারবাইজান

এর বৈশিষ্ট্য লক্ষ্যণীয়। এখানে কোথাও কোনো ছুঁচালো কিনারা নেই—

তথ্য কৃতজ্ঞতা:

১. Mathematicians discover new class of shape seen throughout nature, লেখক: Philip Ball, doi: https://doi.org/10.1038/d41586-024-03099-6

২. Domokos, G., Goriely, A., Horváth, A. G. & Regős, K., PNAS Nexus 3, pgae311 (2024).

চিত্র কৃতজ্ঞতা: Domokos, G., Goriely, A., Horváth, A. G. & Regős, K., PNAS Nexus 3, pgae311 (2024).